- Nodes with no children are known as
leaves; the leaves in the tree below aresiblings; thus, Grandparentandgrandchildrelations can be defined in a similar manner.
- A
pathfrom node - The
lengthof this path is the number of edges on the path, namely,
- For any node ni, the
depthof - The
heightofleaf. Thus all leaves are at height
Implementation of a tree
struct TreeNode {
Object element;
TreeNode *firstChild;
TreeNode *nextSibling;
};
Binary Trees
A binary tree is a tree in which no node can have more than two children.
Binary Search Trees
-
An important application of binary trees is their use in searching.
-
The property that makes a binary tree into a binary search tree is that for every node,
- the values of all the items in its
leftsubtree aresmallerthan the item in - and the values of all the items in its
rightsubtree arelargerthan the item in
- the values of all the items in its
Binary Search Tree: Node
struct Node {
int key;
Node* left;
Node* right;
Node(int item) {
key = item;
left = NULL;
right = NULL;
}
};
Source Code: binary_search_tree.cpp
Binary Search Tree: Insert
Node* insert(Node* node, int key) {
if (node == NULL)
return new Node(key);
if (node->key == key)
return node;
if (node->key < key)
node->right = insert(node->right, key);
else
node->left = insert(node->left, key);
return node;
}
Play at: Tree Visualizer, Source Code: binary_search_tree.cpp
Binary Search Tree: Insert - let's play
Let's try with the following list of elements
100, 164, 130, 189, 244, 42, 141, 231, 20, 153
At the end, verify at: Tree Visualizer
Binary Search Tree: Insert - comments
- The order of insertions will define the form of the tree
- The form of the tree will define the eficiency of searching process
Think about it:
- What would happen if we insert all nodes in order?
1,2,3,4,5,5,6,7,8,9
Check it out at: Tree Visualizer
So, the higher the tree, the less efficient that search will be
Binary Search Tree: Search
Do you remember the binary search algorithm?
Yes, it's the same but with trees
Node* search(Node* root, int val) {
if (root == nullptr || root->key == val) {
return root;
}
if (val < root->key) {
return search(root->left, val);
} else {
return search(root->right, val);
}
}
Binary Search Tree: Delete
There are three cases to consider when deleting a node:
- The target node is a
leaf - The target node has a single
child - The target node has 2
children
Binary Search Tree: Delete - Let's code
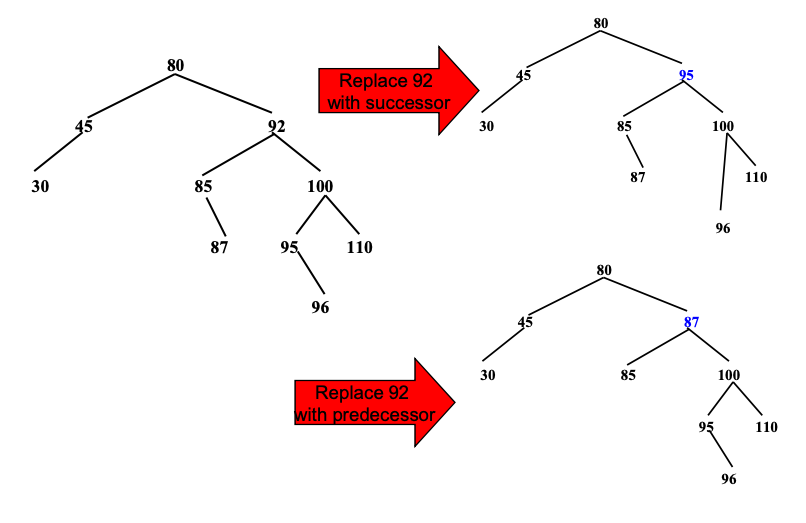
There are 2 ways to arrange a tree after deletion of a node with 2 children.
- Replacing deleted node by its immeditate predecessor
- Replacing deleted node by its immediate successor
In our sample code we implemented the findMin function to help the deleteNode. The findMin will get the in-order minimum successor, and then use it to replace the deleted node.
How would you implement findSuccessor and findPredecessor?
Test with this tree
Remove 8, 3 and 10
Traversals in Binary Trees
Resources and Credits
This material is genereated thanks to some extracts from following resources:
- Weiss, Mark Allen. Data Structures and Algorithm Analysis in C++. 4th ed. Boston: Pearson, 2014.
- Humberto González, Luis. Abstraccion de Datos
- Erickson, Jeff. Algorithms ...
- Google-generated code with
AI Overview
Thanks
- Obed N Muñoz Reynoso
- obed.n.munoz@tec.com
- @obedmr