Sorting Algorithms: Why should we care?

Simple, if we don't sort them, we cannot find it

Think about a list of unsorted phone numbers from the Contacts App in your phone. And also, imagine that you don't have a seach field. How would you find your contacts?

Common Algorithms

• Bubble Sort
• Selection Sort
• Insertion Sort
• MergeSort
• QuickSort
• Shell Sort
• Heap Sort
• Bucket Sort
• .... <your> sort

How we choose the best sorting algorithm?

• Execution time (a.k.a. complexity: , , , ...)
  • Number of comparisons
  • Number of movements
• Data size and structure
• Available resources (memory, cpu, storage ...)
• Data type (strings, numbers, combined, ...)
• What else?

Bubble Sort 1/4

Compares in bubbles (pairs), from the beginning of the array to the end. If the first element of the bubble is bigger, the 2 elements will be swapped.

The above process is repeated through the whole array until there are no more swaps to do.

Its complexity:

• Best Case -
• Worst Case -

Bubble Sort 2/4

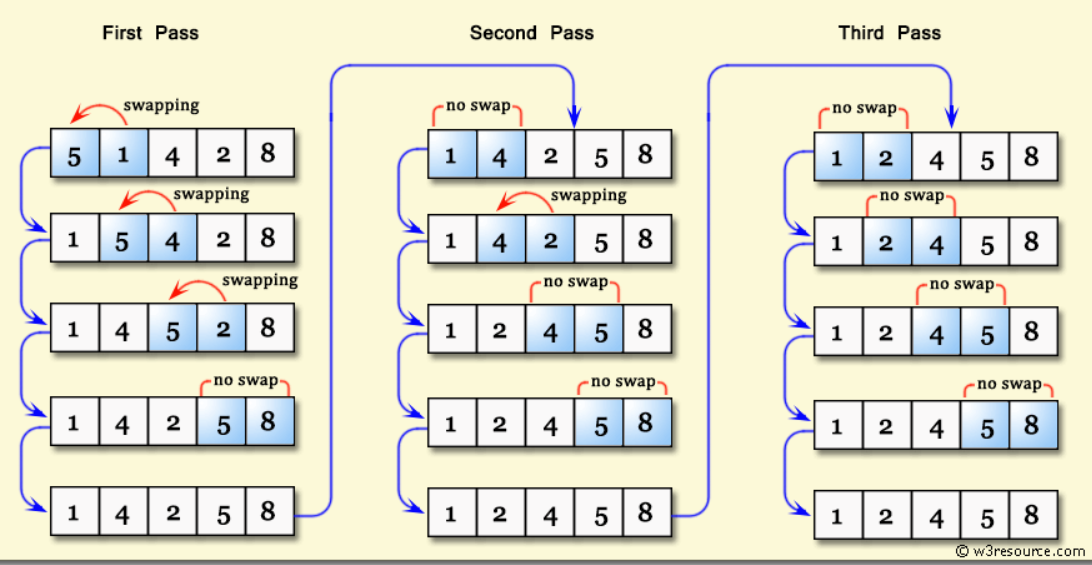
Bubble Sort 3/4

void bubbleSort(std::vector<int>& arr) {
    int n = arr.size();
    bool swapped; // Flag to check if any swaps occurred in a pass

    for (int i = 0; i < n - 1; ++i) {
        swapped = false; // Reset swapped flag for each pass
        for (int j = 0; j < n - 1 - i; ++j) {
            // Compare adjacent elements
            if (arr[j] > arr[j + 1]) {
                // Swap if they are in the wrong order
                std::swap(arr[j], arr[j + 1]);
                swapped = true; // Mark that a swap occurred
            }
        }
        // If no two elements were swapped in inner loop, then array is sorted
        if (swapped == false) {
            break;
        }
    }
}

Bubble Sort 4/4

Quick Excersice:

Given the arr array, calculate the number of comparisons and the number of swaps

std::vector<int> myVector = {64, 347, 5, 12, 212, 11, 920, 64, 37, 25, 72, 22, 96, 90};

Source Code: bubble_sort.cpp

Selection Sort 1/4

It will search for the minimum (or maximum) value in the array, then it will go through the rest of the array and if it finds a smaller value, they will swap their position.

The above process is repeated with all the array, previous sorted values will not be visited anymore.

Its complexity:

• Best/Worst Case -

Selection Sort 2/4

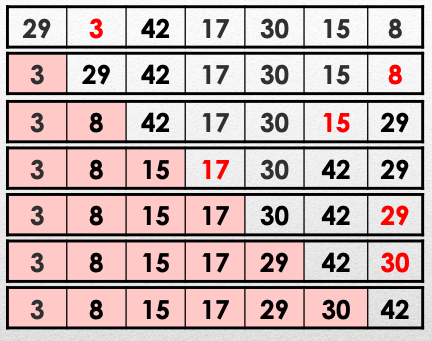
Selection Sort 3/4

void selectionSort(std::vector<int>& arr) {
    int n = arr.size();
    for (int i = 0; i < n - 1; ++i) {
        // Find the minimum element in the unsorted part of the array
        int min_idx = i;
        for (int j = i + 1; j < n; ++j) {
            if (arr[j] < arr[min_idx]) {
                min_idx = j;
            }
        }
        // Swap the found minimum element with the first element of the unsorted part
        if (min_idx != i) {
            std::swap(arr[min_idx], arr[i]);
        }
    }
}

Selection Sort 4/4

Quick Excersice

Is it really ? Let's verify it

Source Code: selection_sort.cpp

Insertion Sort 1/5

The process of sorting an array with insertion sort is similar to how a person might sort a hand of playing cards

Its complexity:

• Best Case -
• Worst Case -

1. The algorithm starts with the first element, which is considered the sorted portion of the array.

2. It then takes the next element (from the unsorted portion) and compares it with the elements in the sorted portion, moving from right to left.

3. As it compares, it shifts any element larger than the current value one position to the right to create a space for insertion.

4. The current element is then inserted into its correct position.

5. This process repeats for each element until the entire array is sorted.

Insertion Sort 4/5

void insertionSort(std::vector<int>& arr) {
    int n = arr.size();
    for (int i = 1; i < n; ++i) {
        int key = arr[i];
        int j = i - 1;

        // Move elements of the sorted subarray that are greater
        // than the key to one position ahead of their current position.
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j = j - 1;
        }
        arr[j + 1] = key;
    }
}

Insertion Sort 5/5

Quick Excersice

What would the worst case scenario?
Write a 5 elements array. You may need to verify it

arr = {   ,   ,   ,   ,   }

Source Code: insertion_sort.cpp

Merge Sort 1/6

This is a recursive algorithm that divides the array by 2 and then sort each one of the in a recursive way.

This algorithm follows the divide-and-conquer principle.

Its complexity:

• Best Case -
• Worst Case -

Merge Sort 3/6

// Recursively divides the array and sorts subarrays
void mergeSort(std::vector<int>& arr, int low, int high) {
    if (low < high) {
        int mid = low + (high - low) / 2; // Calculate the middle index

        // Recursively sort the left and right halves
        mergeSort(arr, low, mid);
        mergeSort(arr, mid + 1, high);

        // Merge the sorted halves
        merge(arr, low, mid, high);
    }
}

Source code: merge_sort.cpp

// Merges two sorted subarrays into a single sorted array
void merge(std::vector<int>& arr, int low, int mid, int high) {
    std::vector<int> temp; // Temporary array for merging
    int left = low;        // Starting index of the left subarray
    int right = mid + 1;   // Starting index of the right subarray

    // Merge elements into the temporary array in sorted order
    while (left <= mid && right <= high) {
        if (arr[left] <= arr[right]) {
            temp.push_back(arr[left]);
            left++;
        } else {
            temp.push_back(arr[right]);
            right++;
        }
    }
    .
    .
    .
}

// Merges two sorted subarrays into a single sorted array
void merge(std::vector<int>& arr, int low, int mid, int high) {

    .
    .
    .

    // Copy any remaining elements from the left subarray
    while (left <= mid) {
        temp.push_back(arr[left]);
        left++;
    }

    // Copy any remaining elements from the right subarray
    while (right <= high) {
        temp.push_back(arr[right]);
        right++;
    }

    // Copy the sorted elements from the temporary array back to the original array
    for (int i = low; i <= high; i++) {
        arr[i] = temp[i - low];
    }
}

Merge Sort 6/6

Quick Excercise

How may sub-arrays would be created in the following array:

arr = [20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1]

Source code: merge_sort.cpp

Quick Sort 1/5

Yet another divide-and-conquer algorithm, but with a pivot

The election of the pivot is free, a simple pivot's choosing technique is just taking the first or the last element of the array.

Then, create 2 sub-arrays, one will contain the smaller values, and other with bigger values than the pivot

Its Complexity

• Average case -
• Worst case -

Quick Sort 3/5

// Main Quicksort function
void quickSort(std::vector<int>& arr, int low, int high) {
    if (low < high) {
        // pi is partitioning index, arr[pi] is now at right place
        int pi = partition(arr, low, high);

        // Separately sort elements before partition and after partition
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

Source code: quick_sort.cpp

Quick Sort 4/5

// Function to partition the array and return the pivot's final index
int partition(std::vector<int>& arr, int low, int high) {
    int pivot = arr[high]; // Choosing the last element as the pivot
    int i = (low - 1);     // Index of smaller element

    for (int j = low; j <= high - 1; j++) {
        // If current element is smaller than or equal to pivot
        if (arr[j] <= pivot) {
            i++; // Increment index of smaller element
            std::swap(arr[i], arr[j]);
        }
    }
    std::swap(arr[i + 1], arr[high]);
    return (i + 1);
}

Quick Sort 5/5

Quick Excercise

Let's figure out what's the best pivot choosing technique (, , or element) for the following array:

arr = [32,14,67,84,39,96,19,32,52,59,1,30,14,97,96,73,55,46,16,19]

Source code: quick_sort.cpp

Let's code: Heap, Shell and Bucket Sort

For a 10,000,000 randomized integers array

• Investigate and implement the HeapSort, ShellSort and BucketSort algorithms
• Add the BubbleSort, SelectionSort, InsertionSort, QuickSort and MergeSort to your program
• Calculate the running time and memory usage for each algorithm to find out which one is the fastest algorithm for the given array
• Explain why the winner algorithm would be the optimal and where it would not be optimal

Resources and Credits

This material is genereated thanks to some extracts from following resources:

• Weiss, Mark Allen. Data Structures and Algorithm Analysis in C++. 4th ed. Boston: Pearson, 2014.
• Humberto González, Luis. Abstraccion de Datos
• Erickson, Jeff. Algorithms ...
• Google-generated code with AI Overview

Thanks

• Obed N Muñoz Reynoso
  • obed.n.munoz@tec.com
  • @obedmr